Volume of a truncated pyramid
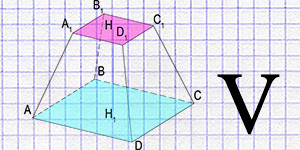
A truncated pyramid is a unique geometric figure obtained by intersecting a regular pyramid with a plane parallel to its base. This intersection cuts off the top part of the pyramid, leaving a figure with two parallel bases of different sizes. Truncated pyramids can be found in many architectural structures, from ancient pyramids to modern buildings. This figure plays an important role not only in architecture but also in many other fields, including mathematics, physics, and engineering.
Historically, truncated pyramids have been used in many cultures around the world. They served not only practical purposes in construction but often also had symbolic or religious significance. In the architecture of ancient civilizations, truncated pyramids could signify places of worship or burial complexes.
From a mathematical perspective, the truncated pyramid is an interesting object due to its properties and variations in shape. Understanding how to calculate the volume of such a figure is important in many practical and theoretical applications. This knowledge is useful not only for professionals in construction and design but also for students studying the basics of geometry.
Geometric Description
A truncated pyramid is a polyhedron formed by intersecting a regular pyramid with a plane parallel to its base. It is characterized by a number of geometric properties:
- A truncated pyramid has two bases - the upper and the lower. Both bases are parallel to each other and can be any polygons of the same shape but different sizes.
- The lateral faces of the truncated pyramid are trapezoids. Their number equals the number of sides of the base.
- The height of the truncated pyramid (h) is the perpendicular dropped from the upper base to the lower base.
- The apothem is the height of the lateral trapezoidal face, drawn from the vertex to the middle of the base side (only for regular truncated pyramids).
Table of Characteristics of a Truncated Pyramid
| Characteristic | Description |
|---|---|
| Bases | Two parallel polygons |
| Lateral Faces | Trapezoids |
| Height | Perpendicular distance between the bases |
| Apothem | Height of the lateral face (for a regular truncated pyramid) |
Mathematical Formulas
The area of the base (S) depends on the shape of the base. For a regular polygon, the formula \( S = \frac{n \times a^2}{4 \times \tan(\frac{\pi}{n})} \) can be used, where n is the number of sides, and a is the side length.
The mathematical formula for calculating the volume of a truncated pyramid is based on the areas of its upper and lower bases, as well as its height. The formula for calculating the volume V of the truncated pyramid is given as:
where:
- S_1 and S_2 are the areas of the upper and lower bases, respectively,
- h is the height of the truncated pyramid, measured as the perpendicular distance between the two bases.
Volume Calculation Example
Consider a truncated pyramid with square bases, where the side of the lower base a_1 = 6 m, the side of the upper base a_2 = 4 m, and the height h = 5 m.
- Area of the lower base S_1 = a_1^2 = 6^2 = 36 \, m^2
- Area of the upper base S_2 = a_2^2 = 4^2 = 16 \, m^2
- Volume of the truncated pyramid: V = \frac{1}{3} \times 5 \times (36 + 16 + \sqrt{36 \times 16}) \approx 141.67 \, m^3
Thus, the volume of this truncated pyramid is approximately 141.67 cubic meters.
Conclusion
The truncated pyramid is a unique geometric figure with interesting properties and a wide range of applications. Calculating the volume of a truncated pyramid is an important skill in geometry, architecture, and engineering. Understanding the principles underlying these calculations helps to gain a deeper insight into spatial structures and their interrelations.
References and Resources
- Stewart, James. "Calculus". Cengage Learning, 2015.
- Lipson, Stephen G. "Stereometry: Understanding Three-Dimensional Geometry". Dover Publications, 2016.
- Aleksandrov, A.D. "Geometry". Moscow: Nauka, 1989.
- Weisstein, Eric W. "MathWorld - A Wolfram Web Resource".
- "Khan Academy - Geometry".
Comments on the calculator

Calculator for accurately calculating the volume of a pyramid using the height and base area or one of the sides of the base.
Go to calculation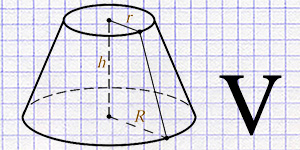
Calculation of the volume of a truncated cone using the radius of the lower and upper bases and height.
Go to calculation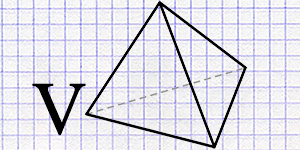
Accurately finding the precise volume of a tetrahedron using edge lengths, radii of inscribed and circumscribed spheres.
Go to calculation