Tetrahedron volume calculator
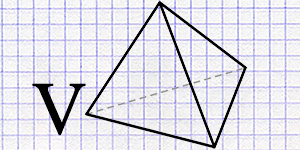
Geometric Description
The tetrahedron is a three-dimensional figure in space, characterized by four triangular faces, four vertices, and six edges. Tetrahedra are divided into different types based on the shape of their faces.
Key elements of a tetrahedron:
| Faces |
Total: 4 faces. Shape: Each face is a triangle. In a regular tetrahedron, all faces are equilateral triangles. |
| Edges |
Total: 6 edges. Features: In a regular tetrahedron, all edges are equal in length. |
| Vertices |
Total: 4 vertices. Features: At each vertex, three faces and three edges converge. |
Types of Tetrahedra:
| Type | Properties |
|---|---|
| Regular (Equilateral) Tetrahedron |
All faces are equilateral triangles. All edges are equal in length. |
| Irregular Tetrahedron |
Faces can be different types of triangles. Edges can have different lengths. |
Geometric Properties:
- In a regular tetrahedron, all angles between the edges are equal, and each angle between the faces is approximately 70.53°.
- The regular tetrahedron has a high degree of symmetry.
- In a tetrahedron, there are no diagonals in the classical sense, as in polyhedra with more than four faces.
These characteristics define the unique properties of the tetrahedron and influence its use in various practical and theoretical applications.
Mathematical Foundations
Different mathematical formulas are used to calculate the volume of a tetrahedron, depending on the type of tetrahedron and the known parameters.
Volume of a Regular Tetrahedron
For a regular tetrahedron, where all sides are equal, the volume \(V\) is calculated using the formula:
where \(a\) is the edge length of the tetrahedron.
Through Height and Base Area
If the height \(h\) of the tetrahedron and the base area \(A\) are known, the volume is calculated as:
Through Edge Lengths
For a tetrahedron with different edge lengths \(a\), \(b\), \(c\), \(d\), \(e\), and \(f\), the volume \(V\) can be calculated using the Cayley-Menger formula:
where \(X = (b^2 + c^2 - e^2)\), \(Y = (a^2 + c^2 - f^2)\), \(Z = (a^2 + b^2 - d^2)\).
Through the Radius of the Inscribed Sphere
If the radius of the sphere inscribed in the tetrahedron \(r_{inscribed}\) is known, then the volume \(V\) of a regular tetrahedron can be found using the formula:
Through the Radius of the Circumscribed Sphere
For a tetrahedron with a known radius of the sphere circumscribed around it \(r_{circumscribed}\), the volume \(V\) is calculated as follows:
Examples of Calculation
- For a regular tetrahedron with an edge length of 4 m, the volume: \(V = \frac{4^3}{6 \sqrt{2}} \approx 9.24\) cubic meters.
- With a height of 5 m and a base area of 10 square meters, the volume: \(V = \frac{1}{3} \times 10 \times 5 = 16.67\) cubic meters.
These formulas allow for the precise calculation of the volume of a tetrahedron, which is an important aspect in many fields, including architecture, engineering, and mathematics.
Practical Application
Tetrahedra find practical applications in architecture, engineering, design, and even art in the modern world. They serve as the basis for creating various structures, from simple decorative objects to complex architectural elements.
Architecture and Construction:
- Tetrahedra are used in architecture to create original and stable structures, such as timber frame houses or playgrounds.
- In construction, tetrahedral elements can be used to reinforce structures and distribute loads.
Design and Art:
- Tetrahedra are applied in interior design and sculptures, providing unique geometric shapes.
- In jewelry art, tetrahedral forms are used to create original ornaments.
Education and Science:
- Calculating the volume of a tetrahedron is an important part of the geometry curriculum.
- In scientific research, tetrahedra are used to model molecular structures and other complex systems.
Games and Entertainment:
- Tetrahedral elements are applied in board and video games, as well as in puzzles.
Conclusion
The tetrahedron, as one of the fundamental geometric figures, plays a significant role in various areas of human activity. From architecture and design to education and scientific research, knowing how to calculate its volume is an important skill. Calculating the volume of a tetrahedron helps to understand complex geometric principles and finds practical application in solving real-world problems. This knowledge contributes to technological development, enhances design and analytical skills, and stimulates a creative approach in various fields of activity.
Comments on the calculator

Calculator for accurately calculating the volume of a pyramid using the height and base area or one of the sides of the base.
Go to calculation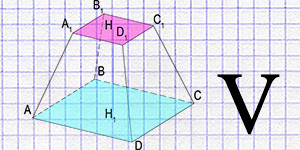
Calculation of the volume of a truncated pyramid through the values of the areas of the bases and height.
Go to calculation
Calculator for accurately calculating the volume of a cone using height or apothem and the base area or base radius.
Go to calculation