Root Calculator
The square root of a number — is one of the fundamental mathematical concepts encountered in various fields of science and engineering. It is the operation inverse to raising a number to a power, allowing to determine a number that, when raised to a certain power, gives a given value. The most well-known are square and cubic roots, although the concept of a root can be extended to any degree.
Historically, the concept of the root dates back to ancient times when mathematicians from Greece and Babylon sought methods for solving quadratic and cubic equations. With the development of mathematics, the concept of the root has been increasingly applied, and today it occupies a central place in many mathematical disciplines, including algebra, geometry, and analysis.
The square root of a number plays a key role not only in theoretical mathematics but also in applied sciences such as physics, engineering, and finance, where it is used to solve a wide range of problems, from calculating distances and areas to determining rates and yields. Understanding and the ability to work with roots open the doors to deep analysis and understanding of the nature of things, making this concept an integral part of mathematical education and scientific research.
Basic Concepts and Definitions
The nth root of a number \(a\) — is such a number \(b\), which when raised to the power \(n\) gives the number \(a\). This concept is written as \(b = \sqrt[n]{a}\), where \(n\) — is the degree of the root, and \(a\) — is the number under the root. For \(n=2\), the root is called square, and for \(n=3\) — cubic. The concept of a root can be extended to any positive integer \(n\).
- Square root of a number \(a\) — is a number \(b\), which when multiplied by itself gives \(a\). It is denoted as \(\sqrt{a} = b\).
- Cubic root from a number \(a\) — is a number \(b\), which when raised to the third power gives \(a\). Denoted as \(\sqrt[3]{a} = b\).
- Positive and negative roots: For any positive number \(a\) and an even \(n\), there are two roots: positive and negative. For example, \(\sqrt{4}\) can be both \(2\) and \(-2\), because \(2^2 = 4\) and \((-2)^2 = 4\).
- Irrational and rational roots: The root of a number can be either irrational or rational. For example, the square root of \(2\) is irrational, and the square root of \(9\) is rational (\(3\)).
- Algebraic properties of roots: Roots adhere to a number of algebraic properties, including properties of multiplication and division (for example, \(\sqrt{a} \times \sqrt{b} = \sqrt{ab}\) and \(\sqrt{a} / \sqrt{b} = \sqrt{a/b}\)), which allows simplifying expressions containing roots.
- Complex roots: For negative numbers in the case of even \(n\), the root is defined in the realm of complex numbers, using the imaginary unit \(i\), where \(i^2 = -1\). For example, \(\sqrt{-4} = 2i\).
Understanding these basic concepts and definitions is necessary for a deep study of the properties of roots and their application in various fields of mathematics and science.
Properties of Roots
Roots of numbers have a number of properties that allow for simplification of calculations and solving mathematical problems. Understanding these properties is key to working with roots in algebra and other areas of mathematics. Below are the main properties of roots:
- Product of Roots: The root of a product is equal to the product of the roots. That is, \(\sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b}\).
- Quotient of Roots: The root of a quotient is equal to the quotient of the roots. This means that \(\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\), provided that \(b \neq 0\).
- Raising a Root to a Power: Raising a root to a power is equal to the root of the number raised to that same power. Thus, \((\sqrt[n]{a})^m = \sqrt[n]{a^m}\).
- Extracting a Root from a Root: Extracting a root from another root can be replaced with a single root, the degree of which is the product of the degrees of the original roots. Example: \(\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}\).
- Rationalizing the Denominator: If a root is present in the denominator of a fraction, it can be "rationalized" by multiplying the numerator and the denominator by the conjugate expression for the denominator, to eliminate the root from the denominator.
- Root of Unity: The n-th root of 1 is equal to 1 for any natural \(n\), that is, \(\sqrt[n]{1} = 1\).
- Roots of Negative Numbers: For even \(n\), the n-th root of a negative number does not exist in the set of real numbers, but exists in the set of complex numbers.
These properties are widely used in simplifying expressions, solving equations and inequalities, and performing other mathematical operations related to roots.
Methods for Calculating Roots with Examples of Formulas
There are various methods for calculating the roots of numbers, both exact and approximate. Here is how these methods can be applied using specific formulas:
- Direct Calculation: For square roots of perfect squares, for example, \(\sqrt{25} = 5\). Cubic roots of perfect cubes can be calculated similarly, for example, \(\sqrt[3]{27} = 3\).
- Using Standard Formulas: Applying properties of roots for simplification, for example, \(\sqrt{a^2} = |a|\) or \(\sqrt[3]{a^3} = a\).
- Bisection Method: Does not have a direct formula, but is used for refining the root by dividing the interval in half and selecting the subinterval that contains the root.
- Newton's Method (Method of Tangents): Iterative formula \(x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\), where \(f(x)\) is the function whose root we are seeking, and \(f'(x)\) is its derivative.
- Using Calculators and Computer Programs: Most calculators and programs use built-in algorithms for calculating roots, the exact formulas of which may vary depending on the software.
- Graphical Method: Not based on a formula, but allows for visually determining an approximate value of the root by finding points of intersection of the function graph with the x-axis.
For each of these methods, it is important to understand the basic principles and be able to apply the corresponding formulas for finding the roots of numbers. Depending on the task and available tools, the most suitable method of calculation can be selected.
Roots of Complex Numbers
Calculating roots from complex numbers is a more complex task than extracting roots from real numbers, but it opens up interesting possibilities in complex analysis and applications. The main formula for finding the roots of a complex number relies on its polar representation.
Let a complex number be \(z = a + bi\), where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit. This number can be represented in polar form as \(z = r(\cos \phi + i\sin \phi)\), where \(r = \sqrt{a^2 + b^2}\) is the modulus of the complex number, and \(\phi = \arctan(\frac{b}{a})\) is its argument.
The \(n\)th root of a complex number \(z\) is defined by de Moivre's formula:
\[ z^{1/n} = r^{1/n}(\cos(\frac{\phi + 2k\pi}{n}) + i\sin(\frac{\phi + 2k\pi}{n})) \]
where \(k = 0, 1, 2, ..., n-1\). This formula gives \(n\) distinct values of the \(n\)th root, corresponding to \(n\) points on the complex plane, evenly distributed around a circle of radius \(r^{1/n}\).
Thus, extracting a root from a complex number leads not to one, but to several possible outcomes, each of which represents a vertex of a regular \(n\)-sided polygon inscribed in a circle on the complex plane. This phenomenon reflects the unique properties of complex numbers and their roots, allowing for deep analysis in various fields of mathematics and physics.
Understanding the roots of complex numbers and being able to work with them opens the door to the world of complex analysis, providing a powerful tool for solving many theoretical and applied problems.
Common Mistakes and Misconceptions
When working with the roots of numbers, especially in the early stages of learning mathematics, it's easy to encounter mistakes and misconceptions that can lead to confusion or incorrect results. Let's consider the most common ones:
- Extracting the root of a negative number: Many students forget that within the realm of real numbers, you cannot take the root of a negative number. This rule stands until the introduction of complex numbers, where the root of a negative number becomes possible.
- Distributive property of roots: A common mistake is trying to apply the distributive property to roots, for example, assuming that \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\). This is incorrect, except in special cases where \(a\) and \(b\) form certain pairs of numbers.
- Errors in operations with roots: Mistakes in simplifying expressions with roots, such as incorrect application of root properties or incorrect simplification of complex radicals, can lead to wrong answers.
- Misconception about roots and powers: Some students confuse the operations of extracting roots and raising to a power, not understanding that these operations are inverses of each other.
- Ignoring complex roots: When studying quadratic equations, it's easy to assume that an equation has no solutions if the radicand is negative. However, with the introduction of complex numbers, it becomes clear that roots exist, but they are complex.
Recognizing and understanding these common mistakes and misconceptions helps avoid them in the future and gain a deeper understanding of the concepts related to the roots of numbers. It's important to continuously practice and consult educational materials or instructors to clarify doubts and difficulties in these topics.
Comments on the calculator
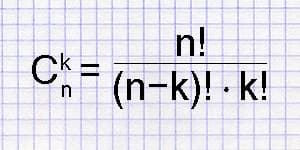
The combinations calculator helps you determine the count of potential combinations from a specified number of objects, denoted as "n choose k."
Go to calculation
The service will help factorize any composite number into its prime factors with a step-by-step solution.
Go to calculation
A Bernoulli trial is a random experiment with two possible outcomes, typically labeled as "success" and "failure".
Go to calculation