Cylinder volume
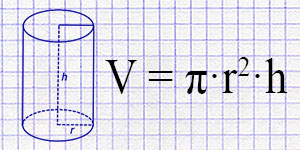
The cylinder is one of the fundamental geometric shapes, playing a significant role in both theoretical mathematics and numerous practical applications. This simple yet versatile form is found in nature, architecture, mechanical engineering, and many other fields. A cylinder is characterized by its straight or curved lateral surface, formed by parallel lines connecting two identical circles or ellipses.
The volume of a cylinder is a key characteristic, crucial for solving a wide range of tasks: from simple calculations in school curriculum to complex engineering calculations in construction and design. Understanding how to calculate the volume of a cylinder can help in various situations - from determining the capacity of a container to calculating materials needed for construction.
Geometric Description of a Cylinder
A cylinder is a three-dimensional geometric figure, characterized by two parallel and equal bases connected by a lateral surface. Here are the key features of a cylinder:
Bases
- Shape: Circular (in the case of a straight circular cylinder) or elliptical (for an elliptical cylinder).
- Location: Parallel to each other at an equal distance.
Lateral Surface
- Shape: A rectangle wrapped around the axis of the cylinder. In a straight cylinder, the lateral surface is perpendicular to the bases.
Height (h)
- Description: The perpendicular distance between the two bases.
- Importance: Determines the length of the lateral surface.
Radius (r) and Diameter (d)
- Radius: The distance from the center of the base to its edge.
- Diameter: Twice the radius, the greatest distance through the central point of the base.
Axis of the Cylinder
- Description: An imaginary line connecting the centers of the bases.
- Role: Determines the direction and orientation of the cylinder.
Types of Cylinders
- Straight Cylinder: The bases are perpendicular to the axis.
- Inclined Cylinder: The bases are tilted relative to the axis.
Table of Cylinder Characteristics
| Characteristic | Description |
|---|---|
| Bases | Two parallel circles of different radii |
| Lateral Surface | Inclined, consists of generators |
| Height (h) | Perpendicular distance between the bases |
| Radii (R and r) | Radii of the larger and smaller bases, respectively |
| Generator (l) | Distance between the edges of the bases |
Mathematical Foundations
Like any other geometric figure, a cylinder has its unique formulas for calculating volume. It's important to understand how these formulas are derived and applied to calculate the volume of a cylinder.
Cylinder Volume Formula
The volume (V) of a cylinder is calculated using the formula:
where:
- r is the radius of the cylinder's base,
- h is the height of the cylinder,
- \(\pi\) is a mathematical constant, approximately equal to 3.14159.
Calculation Principles
- Radius: To find the volume, the radius of the base is needed. The radius is the distance from the center of the circular base to its edge.
- Height: The height of the cylinder is measured as the perpendicular distance between the two bases.
- Using \(\pi\): The constant \(\pi\) is used for calculating the area of the circle, which is then multiplied by the height to obtain the volume.
Calculation Examples
1. Cylinder with a radius of 3 m and height of 5 m:
2. Cylinder with a radius of 2 m and height of 10 m:
These examples illustrate the basic principle of calculating the volume of a cylinder and demonstrate how changes in radius and height affect the volume. It's important to understand these mathematical principles for accurately calculating volumes in various practical tasks.
Practical Application of Calculations
-
Engineering and Construction: Cylinders are widely used in structures of buildings, water towers, gas and liquid storage. Knowing their volume helps in calculating materials and planning space usage.
-
In various industrial sectors, such as oil and gas, chemical, and food industries, cylinders are used as reservoirs and tanks. Calculating their volume is necessary to determine capacity.
-
In medical equipment, such as oxygen cylinders and cylindrical storage containers, volume calculation helps in determining capacity and dosing.
-
In educational institutions, knowledge of calculating the volume of a cylinder is used to teach students the basics of geometry and mathematics.
-
Everyday Life: Calculating the volume of cylindrical objects, such as bottles, cans, and barrels, helps determine their capacity.
Conclusion
The cylinder, as a geometric figure, plays an important role in various areas of our lives. Understanding how to calculate its volume is a key skill in many professional and academic fields. This calculation not only enhances our understanding of geometry but also provides practical utility in engineering, construction, industry, and many other areas. Thus, knowing and being able to apply mathematical formulas to calculate the volume of a cylinder opens doors to solving complex practical tasks and contributes to technological and scientific innovations.
Comments on the calculator

Calculator for accurately calculating the volume of a pyramid using the height and base area or one of the sides of the base.
Go to calculation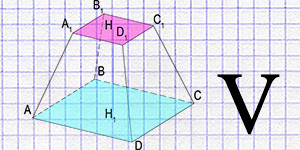
Calculation of the volume of a truncated pyramid through the values of the areas of the bases and height.
Go to calculation
Calculator for accurately calculating the volume of a cone using height or apothem and the base area or base radius.
Go to calculation