Circle Area Calculator

A circle is a set of points on a plane that are all the same distance from a central point, known as the center of the circle. This distance between the center and any point on the circumference of the circle is called the radius. The circle is one of the fundamental geometric figures, and its properties are closely related to the concept of circumference, which represents the boundary of the circle.
Among the basic properties of the circle, the following can be highlighted:
- All points on the circumference are at an equal distance from the center, which defines the circle as a geometric figure.
- The radius is a segment connecting the center of the circle with any point on its circumference. The radius is used in the main formula for calculating the area of a circle.
- The diameter is the longest segment passing through the center of the circle and connecting two points on its circumference. The diameter is equal to twice the radius (\(d = 2r\)).
- The circumference of the circle is the length of the circle's boundary. The formula for the circumference length: \(C = 2\pi r\), where \(\pi\) is the mathematical constant approximately equal to 3.14159.
- The area of the circle is calculated by the formula: \(S = \pi r^2\), where \(S\) is the area, \(r\) is the radius, and \(\pi\) is the mathematical constant.
Formulas for Calculating the Area of a Circle
One of the fundamental tasks in geometry is the calculation of the area of a circle. The area of a circle can be found in various ways, depending on the known parameters.
Derivation of the Circle Area Formula Through Radius
The most common method of calculating the area of a circle is through its radius. If the radius of the circle is \(r\), then the area of the circle (\(S\)) is calculated by the formula:
\[S = \pi r^2\]
where \(\pi\) is a mathematical constant, approximately equal to 3.14159.
Variants of Calculating the Area Through Diameter
The area of a circle can also be calculated through the diameter (\(d\)). Since the diameter is twice the radius (\(d = 2r\)), the formula for the area through the diameter looks like this:
\[S = \pi \left(\frac{d}{2}\right)^2 = \frac{\pi d^2}{4}\]
Calculating the Area of a Circle Through the Circumference Length
If the circumference length (\(C\)) is known, the area of the circle can be found through this parameter. The formula for the circumference length \(C = 2\pi r\), from which the radius \(r = \frac{C}{2\pi}\). Substituting the radius into the area formula, we get:
\[S = \pi \left(\frac{C}{2\pi}\right)^2 = \frac{C^2}{4\pi}\]
Comments on the calculator
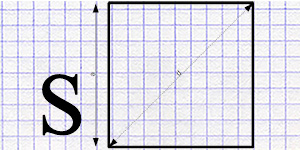
Calculator for computing the area of a square by the length of its side, diagonal, radius of the inscribed and circumscribed circle.
Go to calculation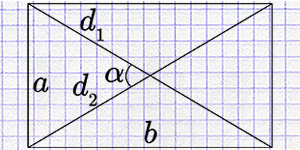
Calculator for computing rectangle area by two sides, diagonal, angle, and radius of the circumscribed circle, among various other methods.
Go to calculation
Calculator for calculating the surface area of the human body based on height and weight values.
Go to calculation